Understanding Binary Cross-Entropy and Log Loss for Effective Model Monitoring

Introduction
Accurately evaluating model performance is essential for understanding how well your ML model is doing and where improvements are needed. Binary Cross-Entropy and Log Loss are two fundamental metrics for this evaluation, especially in classification tasks. Understanding these metrics is not just theoretically important but is a practical necessity for anyone involved in developing or maintaining machine learning models in production.
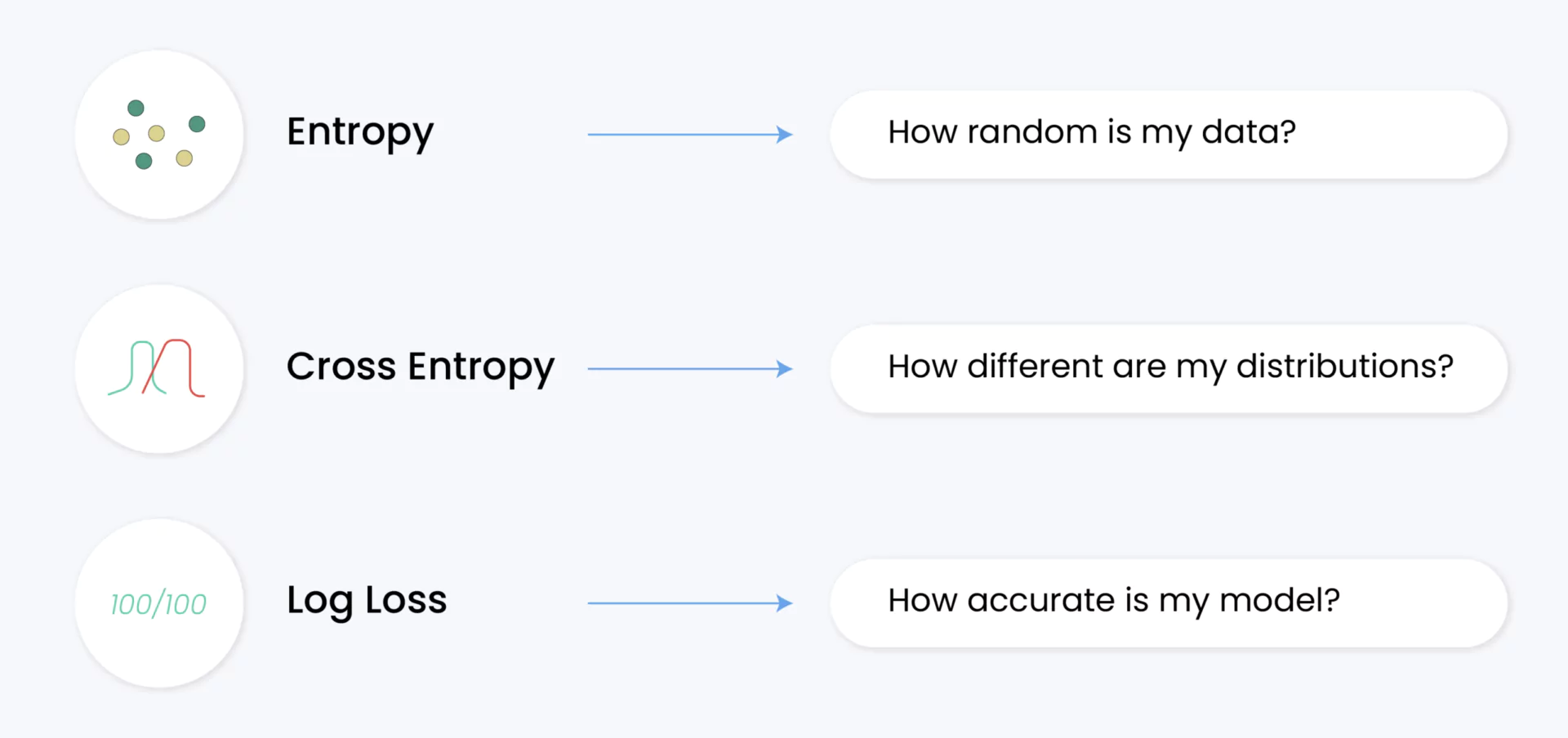
Introducing Binary Cross-Entropy and Log Loss
What are Binary Cross-Entropy and Log Loss?
Binary Cross Entropy and Log Loss refer to the same concept and are used interchangeably. They are loss functions specifically tailored for binary classification problems.
In binary classification, you have two classes, often referred to as the positive class (1) and the negative class (0). Binary Cross Entropy/Log Loss measures the dissimilarity between the actual labels and the predicted probabilities of the data points being in the positive class. It penalizes the predictions that are confident but wrong.
Mathematically, it is expressed as:
- (y * log(p) + (1 - y) * log(1 - p))
where ‘y‘ is the actual label and ‘p‘ is the predicted probability for the data point being in the positive class.
In short, Binary Cross Entropy and Log Loss are two names for the same concept, and they play a crucial role in training models for binary classification by measuring how well the model’s predicted probabilities align with the true labels.
Why are They Crucial for Model Monitoring?
Monitoring these metrics can reveal how well your model’s predictions are aligning with the actual outcomes, which is vital for evaluating its performance over time. They help in understanding whether the model is improving, staying constant, or degrading, which is especially critical in changing environments.
Understanding Binary Cross-Entropy
Information Theory Basics
In information theory, entropy is used to measure the uncertainty or randomness of a set of outcomes. This uncertainty is inherent in the data, and higher entropy means higher unpredictability in the data. The entropy H(X) of a discrete random variable X is defined as:
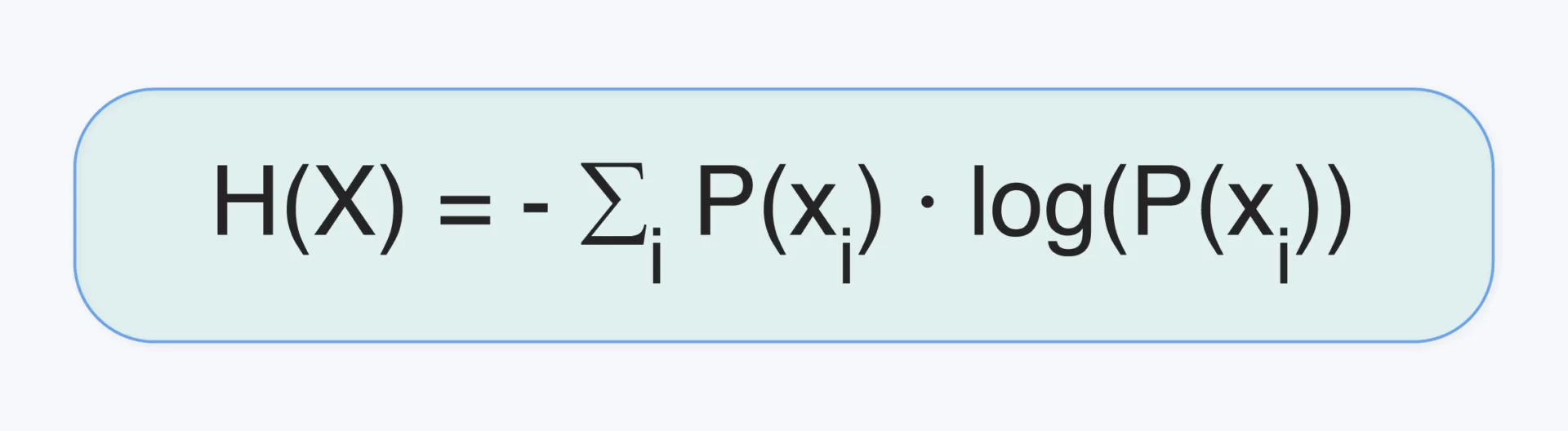
Entropy as a Measure of Uncertainty
Entropy can be seen as a measure of surprise. In the context of machine learning, lower entropy means that the model’s predictions are more reliable, while higher entropy implies more confusion.
How Cross-Entropy Measures the Difference between Two Distributions
Cross-entropy measures the dissimilarity between two probability distributions, ‘P’ and ‘Q’, over the same set of events. It tells you how inefficient your predictions would be when you use them to encode the actual distribution. Cross-entropy H(P, Q) is defined as:
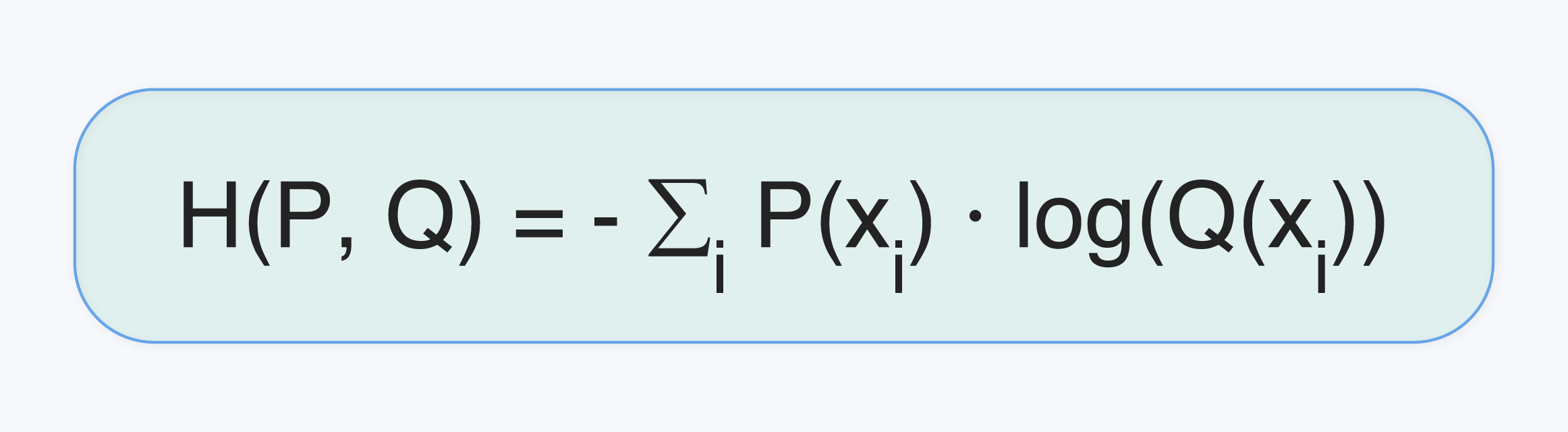
Practical Examples and Interpretation
If ‘Q’ is the same as ‘P’, cross-entropy is equal to entropy. However, as ‘Q’ diverges from ‘P’, cross-entropy increases, indicating that ‘Q’ is a less accurate representation of the data.
For instance, in language modeling, cross-entropy can help measure how likely the predicted next word is compared to the words people actually use next. Lower values are better as they indicate that the predicted distribution is closer to the true distribution.
Zooming in on Binary Cross-Entropy
Special Case: When Target Variable has Only Two Classes
In binary classification, the target variable has only two classes (0 and 1). In this case, binary cross-entropy ‘BCE’ can be defined as:

Where ‘y’ is the true label and ‘p’ is the predicted probability of the sample being in class 1.
It specifically evaluates how well the predicted probabilities of the two classes match the actual classes.
Understanding the Intuition and Interpretation
In practice, Binary Cross-Entropy is very useful for tasks like medical diagnosis, where you need to categorize the output into one of two categories (e.g., disease or no disease), and the confidence of the prediction is crucial.
Use Cases for Binary Cross-Entropy
Binary Cross-Entropy is widely used in training neural networks for binary classification problems. For instance, it’s commonly used in models predicting whether an email is spam or not, whether a credit card transaction is fraudulent, or whether an image contains a particular object.
Understanding Log Loss
Logarithmic Loss Explained
Log Loss extends Binary Cross-Entropy to multi-class classification problems. It takes into account how far the predicted probabilities are from the actual class labels. For ‘n’ samples and ‘m’ different labels, Log Loss ‘L’ is defined as:
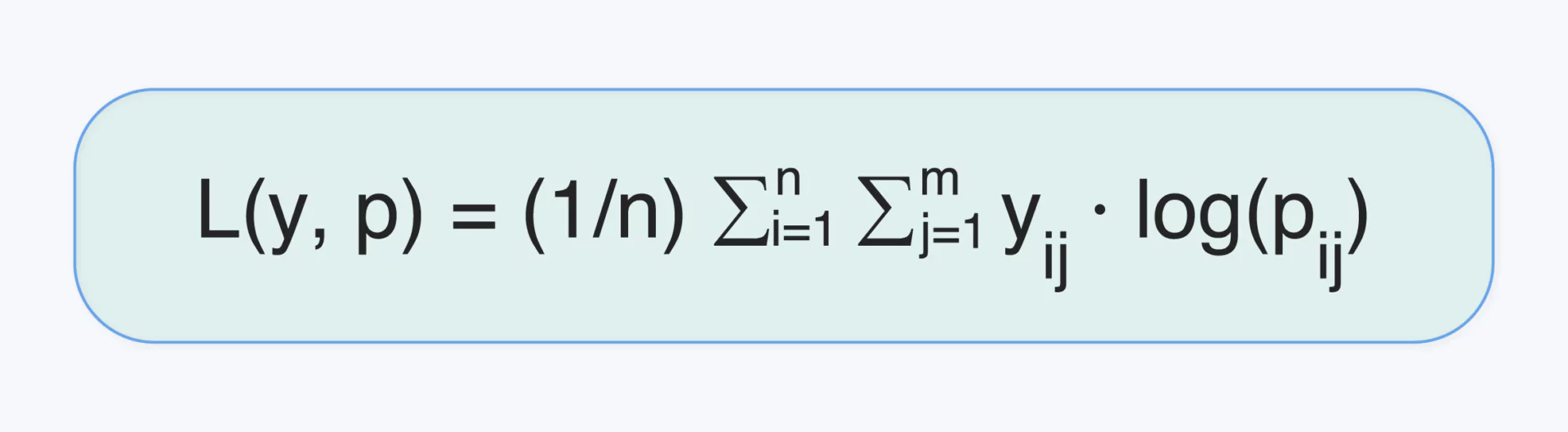
Interpreting Log Loss
A perfect model has a Log Loss of 0. The higher the Log Loss, the worse the model. It’s sensitive to both the direction and magnitude of the predicted probabilities, so it’s especially useful when well-calibrated predicted probabilities are important.
Model Monitoring Using Binary Cross-Entropy and Log Loss
Continuous monitoring of machine learning models in production is essential for ensuring that they maintain high performance and reliability. By monitoring Binary Cross-Entropy and Log Loss, you can track the model’s ability to make confident and accurate predictions.
Setting up alerts based on these metrics can help in identifying when the model might be degrading due to changes in the underlying data distribution or other factors. This continuous monitoring enables timely interventions, such as model retraining or adjustment, to maintain optimal performance.
For example, an increasing log loss trend in a fraud detection model could signal its inability to adapt to novel fraud types.
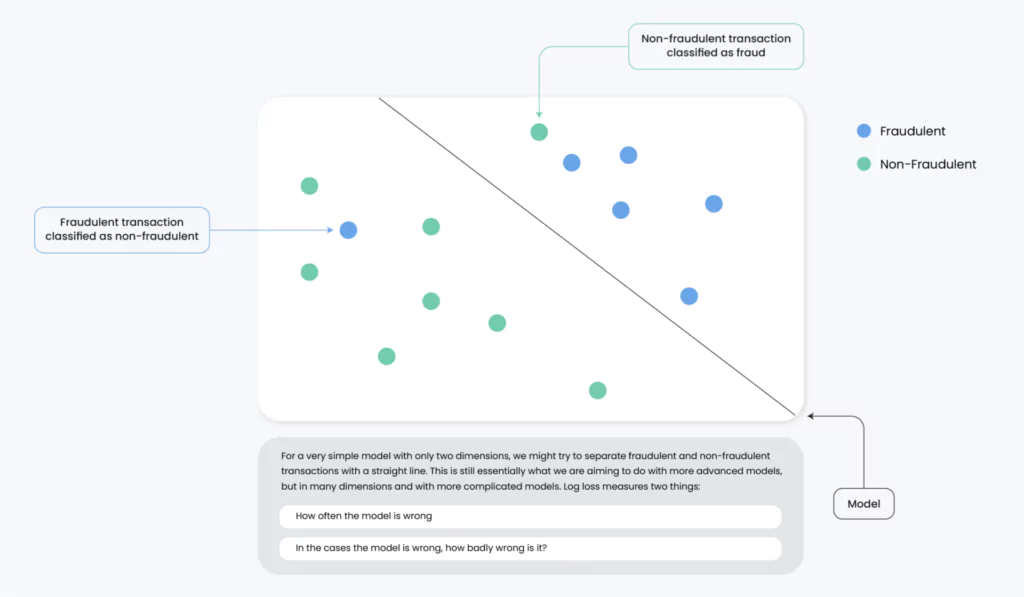
Binary Cross-Entropy and Sigmoid Activation: A Powerful Combination in Neural Networks
The blend of activation functions and loss functions can significantly sway neural network performance. Combining binary cross-entropy as a loss function with a sigmoid activation function in the output layer makes a potent pair for handling binary classification problems.
Sigmoid Activation Function Unveiled
The sigmoid function, a type of activation function, converts any real-valued number into a value between 0 and 1. This feature makes it ideal for models predicting probabilities.
In a neural network, the sigmoid function can represent a neuron’s firing rate, from a state of no firing (0) to a state of fully saturated, maximum frequency firing (1).
Why Binary Cross-Entropy and Sigmoid Pair Well
A neural network learns by adjusting its weights and biases based on the error computed from the previous iteration, using the loss function. Binary cross-entropy often becomes the chosen function for binary classification. Binary cross-entropy and the sigmoid activation function create a synergistic effect in the output layer for the following reasons:
- Probabilistic Output: The sigmoid function ensures the output is a probability, restricting the value between 0 and 1. This perfectly aligns with the binary cross-entropy function, which operates on predicted probabilities.
- Effective Learning Gradient: For efficient learning, the loss function should provide a good gradient. Owing to the mathematical properties of the sigmoid and binary cross-entropy functions, their gradient product is conducive to learning.
- Penalty for Incorrect Predictions: The combined use of these functions effectively penalizes wrong yet confident predictions. If the network makes a wrong prediction with high confidence, the sigmoid function will yield a value close to 0 or 1, leading to a large binary cross-entropy loss due to its logarithmic component.
The binary cross-entropy loss function and sigmoid activation function in a neural network effectively handle binary classification tasks. This demonstrates the synergy achieved when the right activation and loss functions are paired together.
Conclusion
Binary Cross-Entropy and Log Loss are powerful metrics for evaluating the performance of classification models. They offer insights into how well the model’s predictions align with the actual labels. Understanding and effectively using these metrics is critical for anyone involved in developing or managing machine learning models. Whether you are looking to improve the performance of your models or ensure their reliability in production environments, these metrics should be an integral part of your toolkit.




